Origami and Mathematics

Crease patterns

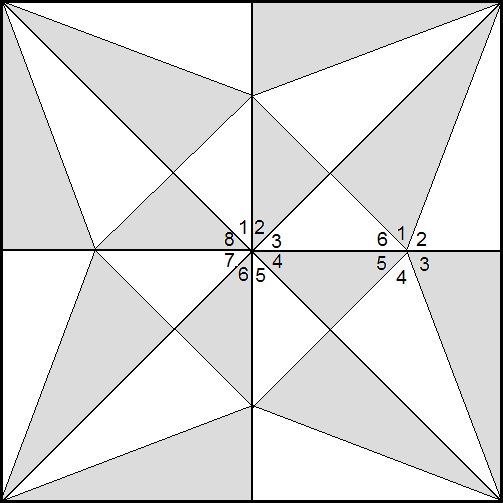
There are a few mathematical theorems involving crease patterns, that is patterns of creases that emerge on a flat sheet of paper while folding. When you unfold an origami model, what you get is a crease pattern.

An example of crease pattern and finished model of a crane

Maekawa's theorem

For every flat-foldable origami model, at any vertex the number of valley and mountain folds always differ by two

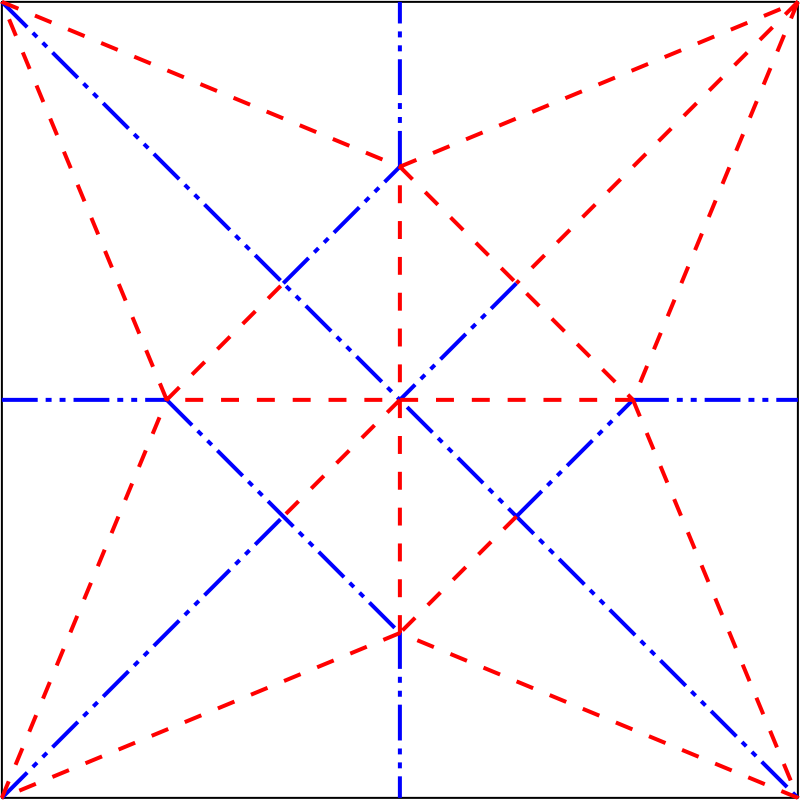
One consequence of Maekawa's theorem is that the total number of folds at each vertex must be an even number. This implies (via a form of planar graph duality between Eulerian graphs and bipartite graphs) that, for any flat-foldable crease pattern, it is always possible to color the regions between the creases with two colors, such that each crease separates regions of differing colors.

When the crease pattern is coloured according to such rules, after folding one side of the model will be entirely of one colour, and the other side will be of the other colour:

Kawasaki's theorem

For every flat-foldable origami model, at any vertex, the sum of all the odd angles adds up to 180 degrees, as do the even.

If and only if these two theorems are true for a model, this model is flat-foldable